TEORI PERILAKU PRODUSEN

Kegiatan 1 Fungsi Produksi

Dalam teori ekonomi, setiap proses produksi mempunyai landasan teknis ,yang disebut fungsi produksi. Fungsi produksi adalah suatu fungsi atau persamaan yang menunjukkan hubungan fisik atau teknis antara jumlah faktor-faktor produksi yang dipergunakan dengan jumlah produk yang dihasilkan per satuan waktu, tanpa memperhatikan harga-harga, baik harga faktor-faktor produksi maupun harga produk. Secara matematis fungsi produksi tersebut dapat dinyatakan:
Y = f (X1, X2, X3, ……….., Xn) ; dimana Y = tingkat produksi (output) yang dihasilkan dan X1, X2, X3, ……, Xn adalah berbagai faktor produksi (input) yang igunakan. Fungsi ini masih bersifat umum, hanya bisa menjelaskan bahwa produk yang dihasilkan tergantung dari faktor-faktor produksi yang dipergunakan, tetapi belum bisa memberikan penjelasan kuantitatif mengenai hubungan antara produk dan faktor-faktor produksi tersebut. Untuk dapat memberikan penjelasan kuantitatif, fungsi produksi tersebut harus dinyatakan dalam bentuknya yang spesifik, seperti misalnya:

a) Y = a + bX ( fungsi linier)
b) Y = a + bX – cX2 ( fungsi kuadratis)
c) Y = aX1bX2cX3d ( fungsi Cobb-Douglas), dan lain-lain.

Dalam teori ekonomi, sifat fungsi produksi diasumsikan tunduk pada suatuMhukum yang disebut : The Law of Diminishing Returns (Hukum Kenaikan Hasil Berkurang). Hukum ini menyatakan bahwa apabila penggunaan satu macam input ditambah sedang input-input yang lain tetap maka tambahan output yang dihasilkan dari setiap tambahan satu unit input yang ditambahkan tadi mula-mula naik, tetapi kemudian seterusnya menurun jika input tersebut terus ditambahkan.

Di bawah ini diberikan satu misal dengan angka-angka hipotetis untuk menunjukkan sifat fungsi produksi seperti yang dinyatakan dalam The Law of Diminishing Returns (Tabel 5.1).
Hubungan produk dan faktor produksi yang digambarkan di atas mempunyai lima sifat yang perlu diperhatikan, yaitu :

(1) Mula-mula terdapat kenaikan hasil bertambah ( garis OB), di mana produk marginal semakin besar; produk rata-rata naik tetapi di bawah produk marginal
(2) Pada titik balik (inflection point) B terjadi perubahan dari kenaikan hasilbertambah menjadi kenaikan hasil berkurang, di mana produk marginal mencapai maksimum( titik B‟); produk rata-rata masih terus naik.
(3) Setelah titik B, terdapat kenaikan hasil berkurang (garis BM), di mana produk marginal menurun; produk rata-rata masih naik sebentar kemudian mencapai maksimum pada titik C‟ , di mana pada titik ini produk rata-rata sama dengan produk marginal. Setelah titik C‟ produk rata-rata menurun tetapi berada di atas produk marginal.
(4) Pada titik M tercapai tingkat produksi maksimum, di mana produk marginal sama dengan nol; produk rata-rata menurun tetapi tetap positif.
(5) Sesudah titik M, mengalami kenaikan hasil negatif, di mana produk marginal juga negatif ; produk rata-rata tetap positif.
Dari sifat-sifat tersebut dapat disimpulkan bahwa tahapan produksi seperti yang dinyatakan dalam The Law of Diminishing Returns dapat dibagi ke dalam tiga tahap, yaitu :
(1) produksi total dengan increasing returns,
(2) produksi total dengan decreasing returns, dan
(3) produksi total yang semakin menurun

Disamping analisis tabulasi dan analisis grafis mengenai hubungan antara produk total, produk rata-rata, dan produk marginal dari suatu proses produksi seperti diatas, dapat pula digunakan analisis matematis. 

Sebagai contoh, misalnya dipunyai fungsi produksi : Y = 12 X2 – 0,2 X3, dimana Y = produk dan X = faktor produksi.

Pertanyaan :
1) Bagaimana bentuk fungsi produk marginal dan fungsi produk rata-ratanya?
2) Kapan fungsi PM dan fungsi PR tersebut mencapai maksimum?
3) Buktikan bahwa kurve produk marginal akan memotong kurve produk rata-rata
pada saat kurve produk rata-rata mencapai maksimum.

Jawaban:
1) Fungsi produk marginal : PM = Y/ X = 24 X – 0,6 X2.
    Fungsi produk rata-rata : PR = Y/X = 12 X – 0,2 X2.
2) Suatu fungsi akan mencapai maksimum apabila turunan pertama dari fungsi
yang bersangkutan sama dengan nol, sedang turunan kedua adala negatif. Jadi,
produk marginal (PM) akan mencapai maksimum, apabila (PM)/ X = 0 dan
( PM)/ X2 = negatif. (PM)/ X = 24 – 1,2 X = 0; X = 20. Jadi, pada saat X =

Dari Tabel 5.1 terlihat, bahwa setiap penambahan faktor produksi satu satuan, mula-mula terdapat tambahan produk (kenaikan hasil) bertambah ( 30, 40 dan 50 satuan), kemudian diikuti oleh tambahan produk (kenaikan hasil) berkurang (50, 40,30,22,8, -2 dan –4). Jika hubungan antara produk total (PT), produk marginal (PM) dan produk rata-rata (PR) pada tabel diatas digambarkan dalam grafik, maka diperoleh grafik seperti Gb.5.1 berikut.

Hubungan produk dan faktor produksi yang digambarkan di atas mempunyai lima sifat yang perlu diperhatikan, yaitu :

(1) Mula-mula terdapat kenaikan hasil bertambah ( garis OB), di mana produk marginal semakin besar; produk rata-rata naik tetapi di bawah produk marginal.

(2) Pada titik balik (inflection point) B terjadi perubahan dari kenaikan hasil bertambah menjadi kenaikan hasil berkurang, di mana produk marginal mencapai maksimum( titik B‟); produk rata-rata masih terus naik.

(3) Setelah titik B, terdapat kenaikan hasil berkurang (garis BM), di mana produk marginal menurun; produk rata-rata masih naik sebentar kemudian mencapai maksimum pada titik C‟ , di mana pada titik ini produk rata-rata sama dengan produk marginal. Setelah titik C‟ produk rata-rata menurun tetapi berada di atas produk marginal.

(4) Pada titik M tercapai tingkat produksi maksimum, di mana produk marginal sama dengan nol; produk rata-rata menurun tetapi tetap positif.

(5) Sesudah titik M, mengalami kenaikan hasil negatif, di mana produk marginal juga negatif ; produk rata-rata tetap positif.

Dari sifat-sifat tersebut dapat disimpulkan bahwa tahapan produksi seperti yang dinyatakan dalam The Law of Diminishing Returns dapat dibagi ke dalam tiga tahap, yaitu :

(1) produksi total dengan increasing returns,

(2) produksi total dengan decreasing returns, dan

(3) produksi total yang semakin menurun

Disamping analisis tabulasi dan analisis grafis mengenai hubungan antara produk total, produk rata-rata, dan produk marginal dari suatu proses produksi seperti diatas, dapat pula digunakan analisis matematis. 

Sebagai contoh, misalnya dipunyai fungsi produksi : Y = 12 X2 – 0,2 X3, dimana Y = produk dan X = faktor produksi.

Pertanyaan :

1) Bagaimana bentuk fungsi produk marginal dan fungsi produk rata-ratanya?

2) Kapan fungsi PM dan fungsi PR tersebut mencapai maksimum?

3) Buktikan bahwa kurve produk marginal akan memotong kurve produk rata-rata pada saat kurve produk rata-rata mencapai maksimum.

Jawaban:

1) Fungsi produk marginal : PM = Y/ X = 24 X – 0,6 X2.

    Fungsi produk rata-rata : PR = Y/X = 12 X – 0,2 X2.

2) Suatu fungsi akan mencapai maksimum apabila turunan pertama dari fungsi yang bersangkutan sama dengan nol, sedang turunan kedua adala negatif. Jadi, produk marginal (PM) akan mencapai maksimum, apabila (PM)/ X = 0 dan ( PM)/ X2 = negatif. (PM)/ X = 24 – 1,2 X = 0; X = 20. Jadi, pada saat X = 20, PM mencapai maksimum. PR akan mencapai maksimum apabila (PR)/ X = 0 dan ( PR)/ X2 = negatif. (PR)/ X = 12 – 0,2 X = 0 . X = 30. Jadi, pada saat X = 30, PR akan mencapai maksimum.

3) PR maksimum = 12 (30) – 0,2 (302) = 180. Pada penggunaan X = 30 , PM = 24 (30) – 0,6 (302) = 720-540 = 180. Jadi, pada saat penggunaan X = 30, PM = PR = 180. Dengan demikian, terbukti bahwa fungsi PM memotong fungsi PR pada saat PR mencapai maksimum.

Elastisitas Produksi dan Daerah-Daerah produksi

Elastisitas produksi adalah rasio perubahan relatif jumlah output yang dihasilkan dengan perubahan relatif jumlah input yang dipergunakan. Atau dapat ditulis :

Misalnya, perubahan output yang dihasilkan akibat perubahan jumlah input sebesar 10% adalah 20%, maka elastisitas produksinya adalah 2 (dua). Elastisitas produksi juga dapat ditulis secara matematis sebagai berikut:

Dari persamaan matematis tersebut, nampak adanya hubungan antara elastisitas produksi dengan produk marginal dan produk rata-rata,sebagai berikut:

1) Jika tingkat produksi di mana PM > PR maka EP > 1

2) Jika tingkat produksi di mana PM = PR maka EP = 1

3) Jika tingkat produksi di mana PM = 0 maka EP = 0

4) Jika tingkat produksi di mana PM negatif maka EP juga negatif.

Berdasarkan nilai elastisitas produksi ini, proses produksi dapat dibagi ke dalam tiga daerah produksi, yaitu :

(a) Daerah dengan EP > 1 sampai EP = 1. Daerah ini dinamakan daerah tidak rasional (irrational stage of production) dan ditandai sebagai Daerah I dari produksi. Pada daerah ini belum akan tercapai keuntungan maksimum, sehingga keuntungan masih dapat diperbesar dengan penambahan input.

b) Daerah dengan EP = 1 sampai EP = 0. Daerah ini dinamakan daerah rasional ( rational stage of production) dan ditandai sebagai Daerah II dari produksi. Pada daerah ini akan dicapai keuntungan maksimum.

(c) Daerah dengan EP = 0 sampai EP < 0. Daerah ini juga dinamakan daerah tidak rasional dan ditandai sebagai Daerah III . Pada daerah ini penambahan input justru akan mengurangi keuntungan.

Daerah-daerah produksi tersebut dapat ditunjukkan secara grafis seperti dalam Gb.

5.2 berikut.

Kegiatan 2 Fungsi Produksi Dengan Satu Faktor Produksi

Fungsi produksi dengan satu faktor produksi adalah hubungan antara tingkat produksi dengan satu macam faktor produksi yang digunakan , sedangkan faktor-faktor produksi yang lain dianggap penggunaannya tetap pada tingkat tertentu (ceteris paribus). Secara matematis fungsi produksi tersebut dapat dinyatakan :

Y = f (X1/X2, X3, ….., Xn)

Fungsi ini dibaca : produk Y adalah fungsi dari faktor produksi X1, jika faktor-faktor produksi X2, X3, ……, Xn ditetapkan penggunaannya pada suatu tingkat tertentu.

Jadi, satu-satunya faktor produksi yang dapat diubah jumlah penggunaannya adalah faktor produksi X1.

Di dalam mempelajari fungsi produksi terdapat tiga ukuran penting yang perlu diperhatikan, yaitu (1) Produk Total (PT), (2) Produk Rata-Rata (PR), dan (3) Produk Marjinal (PM). Produk Total adalah tingkat produksi total ( = Y , dalam fungsi produksi diatas). Produk Rata-Rata adalah hasil rata-rata per unit input variabel ( = Y/X). Produk Marjinal adalah tambahan output yang dihasilkan dari tambahan satu unit input variabel ( Y/ X atau Y/ X). Untuk menganalisis fungsi produksi tersebut perlu dipahami kurve-kurve yang berkaitan dengan ketiga ukuran di atas, yaitu ( lihat Gb. 5.1 ):

(1) Kurve Produk Total (KPT) atau Total Physical Product Curve (TPP) yaitu kurva yang menunjukkan tingkat produksi total (=Y) pada berbagai tingkat penggunaan input variabel.

(2) Kurve Produk Rata-Rata (KPR) atau Average Physical Product Curve (APP), yaitu kurve yang menunjukkan hasil rata-rata per unit input variabel pada berbagai tingkat penggunaan input tersebut.

(3) Kurve Produk Marginal (KPM) atau Marginal Physical Product Curve (MPP), yaitu kurve yang menunjukkan tambahan output (Y) yang disebabkan oleh penggunaan tambahan satu unit input variabel.

Efisiensi dan Produksi Optimum

Konsep efisiensi dapat dipandang dari dua aspek, yaitu dari aspek teknis dan dari aspek ekonomis. Konsep efisiensi dari aspek teknis dinamakan konsepb efisiensi teknis. Efisiensi teknis maksimum dicapai pada saat dicapai produk ratarata maksimum. Tingkat pemakaian faktor produksi yang menghasilkan produk ratarata maksimum, secara teknis dipandang sebagai tingkat produksi optimum. Untuk menentukan tingkat efisiensi dan produksi optimum secara teknis ini cukup dengan diketahuinya fungsi produksi.

Konsep efisiensi dari aspek ekonomis dinamakan konsep efisiensi ekonomis atau efisiensi harga. Dalam teori ekonomi produksi, pada umumnya menggunakan konsep ini. Dipandang dari konsep efisiensi ekonomis, pemakaian faktor produksi dikatakan efisien apabila ia dapat menghasilkan keuntungan maksimum. Untuk menentukan tingkat produksi optimum menurut konsep efisiensi ekonomis, tidak cukup hanya dengan mengetahui fungsi produksi. Ada syarat lagi yang harus diketahui, yaitu rasio harga harga input-output. Secara matematis,

syarat tersebut adalah sebagai berikut. 

Keuntungan (p) dapat ditulis :

Jadi jelaslah bahwa untuk menentukan tingkat produksi optimum menurut konsep efisiensi ekonomis diperlukan dua syarat , yaitu:

(1) Syarat keharusan (necessary condition) : hubungan teknis antara produk dan faktor produksi atau fungsi produksi;

(2) Syarat kecukupan (sufficiency condition) : nilai produk marginal dari faktor produksi yang dipakai harus sama dengan harga satuan faktor produksi itu.

Berikut ini diberikan contoh menentukan tingkat produksi optimum. Misalnya, diketahui fungsi produksi seperti yang tertera pada tabel 5.1. Harga satuan faktor produksi (Px) adalah Rp. 2000,- dan harga satuan produk (PY) adalah Rp. 100,-.

Pertanyaan :

1) Berapa satuankah faktor produksi yang harus digunakan agar dicapai

keuntungan maksimum?

2) Berapa produksi optimumnya?

3) Berapa tingkat keuntungan maksimumnya?

Jawaban:

1) NPM yang terdekat dengan Px adalah Rp. 2.200,-, yaitu Rp.100,- x 22 (PM).

Nilai ini diperoleh dari pemakaian faktor produksi antara 6 dan 7. Jadi, pemakaian faktor produksi yang memberikan keuntungan maksimum adalah antara 6 dan 7. Jika faktor produksi tidak dapat dipecah-pecah maka penggunaan faktor produksi dapat ditetapkan 7 satuan.

2) Berdasarkan jawaban no. 1) diatas, produksi optimumnya adalah antara 21dan 232 atau 232 jika digunakan faktor produksi 7 satuan.

3) Keuntungan maksimumnya : ( Rp.100) (232) – (Rp.2000,-) (7) = Rp.9.200,-.

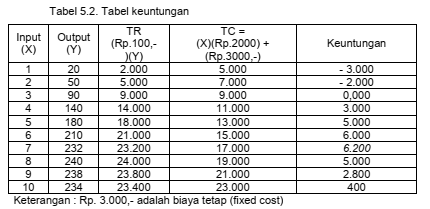
Selain melalui pendekatan tabel seperti di atas, untuk menentukan tingkat produksi optimum dapat pula melalui pendekatan grafis sebagai berikut. Dari tabel 5.1 dapat diperoleh tabel 5.2 sebagai dasar menentukan tingkat produksi optimal secara grafis.

Dari tabel 5.2 dapat diketahui bahwa keuntungan paling besar adalah Rp. 6.200,-, dengan total output 232, pada penggunaan input 7 satuan. Secara grafis perhitungan tersebut dapat digambarkan seperti pada Gb. 5.3. Kurve TVP ( Total Value Product) menunjukkan hubungan antara input X dan TR ( Total Revenue).

Kurve TFC (Total Factor Cost) atau TIC (Total Input Cost) menunjukkan hubungan antara input X dengan TC ( Total Cost). Keuntungan maksimum dicapai jika jarak vertikal antara TVP dan TFC adalah terbesar. Posisi ini ditemukan pada tingkat penggunaan input di mana garis singgung dari TVP sejajar dengan TFC. Pada Gb. 5.3 terlihat bahwa keuntungan maksimum diperoleh pada penggunaan input 7 satuan.